Trabalho

 

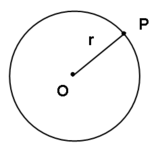
CircunferênciaEditar

Seja ${\displaystyle O\,\!}$ um ponto qualquer do plano e ${\displaystyle r>0\,\!}$ um número real. A circunferência de centro ${\displaystyle O\,\!}$ e raio ${\displaystyle r\,\!}$ é o lugar geométrico dos pontos ${\displaystyle P\,\!}$ desse plano tais que ${\displaystyle PO=r\,\!.}$

Arco de circunferência Editar

Consideremos uma circunferência {\displaystyle \lambda \,\!}{\displaystyle \lambda \,\!} de centro {\displaystyle O\,\!.}{\displaystyle O\,\!.} Sejam {\displaystyle A\,\!}{\displaystyle A\,\!} e {\displaystyle B\,\!}{\displaystyle B\,\!} dois pontos distintos de {\displaystyle \lambda \,\!.}{\displaystyle \lambda \,\!.}

Circ6.png

Um arco de circunferência de extremos {\displaystyle A\,\!}{\displaystyle A\,\!} e {\displaystyle B\,\!}{\displaystyle B\,\!} {\displaystyle ({\widehat {AB}})}{\displaystyle ({\widehat {AB}})} é cada uma das partes em que fica dividida uma circunferência por dois de seus pontos.

Quando {\displaystyle A\equiv B}{\displaystyle A\equiv B} teremos dois arcos: o arco nulo (um ponto) e o arco de uma volta (uma circunferência).

Circ7.png

Arco de circunferência e ângulo central correspondente Editar

{\displaystyle med(A{\widehat {O}}B)=\alpha }{\displaystyle med(A{\widehat {O}}B)=\alpha }

A medida de um arco é, por definição, a medida do ângulo central correspondente. Medir significa comparar com uma unidade padrão previamente adotada. Contudo, para evitar possíveis divergências na escolha da unidade para medir um mesmo arco, as unidades de medida restringem-se a três principais: o grau ({\displaystyle \ ^{\circ }\,\!}{\displaystyle \ ^{\circ }\,\!}), o radiano ({\displaystyle rad\,\!}{\displaystyle rad\,\!}) e o grado, sendo este último não muito comum.

O grau Editar

Hypotenusa.png

Um grau é um arco de circunferência cujo comprimento equivale a {\displaystyle {\frac {1}{360}}}{\displaystyle {\frac {1}{360}}} da circunferência que contém o arco a ser medido. Portanto, a medida, em graus, de um arco de uma volta completa (uma circunferência) é {\displaystyle 360^{\circ }.}{\displaystyle 360^{\circ }.}

Submúltiplos do grau

O minuto {\displaystyle (^{\prime }):}{\displaystyle (^{\prime }):} {\displaystyle 1^{\prime }={\frac {1}{60}}\cdot 1^{\circ },}{\displaystyle 1^{\prime }={\frac {1}{60}}\cdot 1^{\circ },} ou seja, {\displaystyle 1^{\circ }=60^{\prime }.}{\displaystyle 1^{\circ }=60^{\prime }.}

O segundo {\displaystyle (^{\prime \prime }):}{\displaystyle (^{\prime \prime }):} {\displaystyle 1^{\prime \prime }={\frac {1}{60}}\cdot 1^{\prime },}{\displaystyle 1^{\prime \prime }={\frac {1}{60}}\cdot 1^{\prime },} ou seja, {\displaystyle 1^{\prime }=60^{\prime \prime }}{\displaystyle 1^{\prime }=60^{\prime \prime }} e {\displaystyle 1^{\circ }=3600^{\prime \prime }.}{\displaystyle 1^{\circ }=3600^{\prime \prime }.}

O radiano Editar

Um radiano é um arco de circunferência cujo comprimento é igual ao raio da circunferência que contém o arco a ser medido. É a unidade do Sistema Internacional (SI).

Conseqüentemente, para medir um ângulo {\displaystyle a{\widehat {O}}b}{\displaystyle a{\widehat {O}}b} em radianos, convém calcular a razão entre o comprimento {\displaystyle l\,\!}{\displaystyle l\,\!} do arco pelo raio {\displaystyle r\,\!,}{\displaystyle r\,\!,} ou seja, calcular quantos radianos mede o arco {\displaystyle {\widehat {AB}}.}{\displaystyle {\widehat {AB}}.} Portanto, como consequência da definição de radiano, podemos estabelecer a seguinte relação:

{\displaystyle \alpha ={\frac {l}{r}},}{\displaystyle \alpha ={\frac {l}{r}},} onde {\displaystyle l\,\!}{\displaystyle l\,\!} e {\displaystyle r\,\!}{\displaystyle r\,\!} devem estar na mesma unidade de comprimento.

O comprimento de uma circunferência de raio {\displaystyle r\,\!}{\displaystyle r\,\!} é {\displaystyle 2\pi r\,\!.}{\displaystyle 2\pi r\,\!.} Logo, a medida do arco de uma volta completa, em radianos, é {\displaystyle {\frac {2\pi r}{r}}=2\pi rad\approx 6,283184.}{\displaystyle {\frac {2\pi r}{r}}=2\pi rad\approx 6,283184.} Para converter unidades, podemos usar as correspondências {\displaystyle 180^{\circ }=\pi rad}{\displaystyle 180^{\circ }=\pi rad} ou {\displaystyle 360^{\circ }=2\pi rad}{\displaystyle 360^{\circ }=2\pi rad} e uma regra de três simples.